15. El �rea de poligonos regulares
Hasta ahora se han visto las f�rmulas para determinar el �rea de
pol�gonos de tres y cuatro lados (tri�ngulos y algunos cuadril�teros,
respectivamente), pero tambi�n hay figuras de cinco, seis, siete,
n lados y de forma regular e irregular.
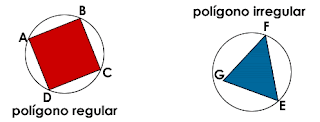
Un pol�gono regular es una figura que tiene sus lados iguales y sus �ngulos congruentes (de igual medida).
Para determinar la f�rmula del pol�gono regular de cinco lados (pent�gono) se hacen las siguientes consideraciones:
pero el t�rmino 5 � b determina el per�metro (p) del pent�gono y "h" es el apotema (a), en consecuencia:
esto significa que el �rea de un pent�gono regular es igual al semiproducto del per�metro por el apotema.
Con esta f�rmula puede hallarse el �rea de cualquier pol�gono
regular conociendo su apotema y la medida de uno de sus lados (su
per�metro se obtiene multiplicando su n�mero de lados por la medida de
uno de ellos); por esto se le conoce como la f�rmula general para
obtener el �rea de un pol�gono regular.
Por otro lado, al construir pol�gonos cada vez con m�s lados,
�stos tienden a formar una circunferencia, la cual es el per�metro de un
c�rculo y su apotema es el radio.
Una circunferencia se define como una l�nea curva cerrada y plana cuyos puntos equidistan de un punto interior llamado centro.
El radio (r) es el segmento de recta que une el centro con un punto cualquiera de una circunferencia.
Di�metro (D) es el segmento de recta que une dos puntos de una
circunferencia pasando por el centro y su longitud equivale a dos veces
la longitud de un radio D = 2 r.
Hechas las consideraciones anteriores, la f�rmula del �rea de un
c�rculo se deduce a partir de la f�rmula general para hallar el �rea de
un pol�gono de
n lados.
Se sustituye el per�metro (p) por la longitud de la circunferencia (2  r) y el apotema (a) por el radio (r), esto es:
r) y el apotema (a) por el radio (r), esto es:
Se desea comprar un terreno para construir un lienzo charro que tenga un radio de 20 m. �Cu�l deber� ser el �rea del terreno?
Contributions to http://dibutec.wikispaces.com/ are licensed under a Creative Commons Attribution Share-Alike 3.0 License. 
Las partes no contribuidas por los visitantes son propieaded intelectual 2013 Tangient
Las partes no contribuidas por los visitantes son propieaded intelectual 2013 Tangient
| sábado, 27 de octubre de 2007 |
| Números al final del periodo |
| Sí, vale, lo de ayer
era una broma. :-) Pero lo cierto es que es uno de los recuerdos más
vivos que tengo del profesor de matemáticas de COU, que nos enseñó esa
"demostración" y a quien yo creí durante un tiempo a pesar de ser una
locura. Otra de las cosas felices que me dieron las matemáticas en aquella época, no sé si en COU o en algún año de BUP, fue mi descubrimiento —junto con Ignacio— de los números al final el periodo. Estábamos en lo alto del puente romano y, lo estoy viendo ahora, en un folio doblado de los que yo usaba para escribir todo le expuse el siguiente método para calcular pi (π), una de mis aficiones de entonces: La idea del método era muy obvia: cuando más lados tenga un polígono regular inscrito en una circunferencia, la suma de la longitud de esos lados se irá aproximando, cada vez más, a la longitud de esa circunferencia. Por ello, lo primero que hacemos es calcular la longitud de un lado para un polígono regular inscrito de n lados (en el dibujo, como dibujé entonces, un hexágono):  Sabemos que, si unimos cada vértice del polígono con el centro, tenemos n triangulitos (no lo he pintado en la figura de lo obvio que es). Si los ángulos de un triángulo suman siempre 180º, tenemos que la suma de los ángulos de los n triangulitos es 180 n; y si le restamos los ángulos cuyo vértice es el centro de la circunferencia (angulos que suman 360º), tenemos que los ángulos que forman los lados del polígno suman 180 n - 360. Como el polígono es regular, cada uno de sus ángulos mide lo mismo, por lo que concluimos, sin mirar a la Wikipedia, que el ángulo de un polígono vale: ángulo = ( 180 n - 360 ) / n = 2 ao lo que es lo mismo: a = ( 180 n - 360 ) / 2n = 90 - 180 / nSi decimos que el lado del polígono mide L y el radio de la circunferencia mide 1, entonces: L / 2 = cos ( a ) = cos ( 90 - 180 / n )y la suma de todos los lados será: n · L = 2 n · cos ( 90 - 180 / n )Dado que nuestro polígono de muchos lados se acerca tanto a la circunferencia y esta tiene una longitud de 2π, nos encontramos con que, si n es muy grande, entonces 2 n · cos ( 90 - 180 / n ) se acercará a 2π, lo que, simplicando, nos da lo siguiente: π = n · cos ( 90 - 180 / n)Esto quizá no sea muy útil en sí mismo, porque, si a lo bruto cambiamos n por infinito, tenemos: infinito · cos ( 90 - 0) = infinito · 0 = indeterminadoPero bueno, la gracia del tema es que teníamos el siguiente número: a = 90 - 180 / ny para valores altos de n —por ejemplo, potencias de 10— tendríamos los siguientes valores de a : Si n = 100.000.000, entonces a = 89,9999982Esto me llevó a la generalización de que si n era una potencia infinita de 10, entonces a tendría la siguiente forma: _He aquí me gran descubrimiento para las matemáticas: que en ocasiones había número después del periodo. Lo que no pensé entonces es que: _ _que suena tan elegante. Wikipedia |
zarevitz | 13:58 || 5 comentarios |
| jueves, 25 de octubre de 2007 |
| Así me lo aprendí yo |
| ¿Cuánto suma 1 + 2 + 4 + 8 + 16 + ··· y así hasta el infinito? Veamos: S = 1 + 2 + 4 + 8 + 16 + ··· |
zarevitz | 22:14 || Sin comentarios |
| martes, 23 de octubre de 2007 |
| El físico también importa |
Un pensamiento por el físico que se nos casa.
|
zarevitz | 18:47 || Sin comentarios |
construcción de polígonos
Haciendo click sobre la imagen, puedes reproducir construcción de polígonos, un video sobre construir-poligonos-regla-compas publicado por Mach425 el el 14 de noviembre de 2008. proceso para construir polígonos regulares con regla y compás.
Ver video "construcción de polígonos"Trazo de polígonos regulares.MOV
Haciendo click sobre la imagen, puedes reproducir Trazo de polígonos regulares.MOV, un video sobre construir-poligonos-regla-compas publicado por DelfusPeru el el 07 de abril de 2011. Este video muestra cómo dibujar un polígono regular utilizando, regla, compás y transportador.
Ver video "Trazo de polígonos regulares.MOV"Polígonos Básicos Regla y compás
Haciendo click sobre la imagen, puedes reproducir Polígonos Básicos Regla y compás, un video sobre construir-poligonos-regla-compas publicado por Adolfo Galindo Borja el el 25 de octubre de 2012. Construcción de perpendiculares, paralelas y polígonos básicos con regla sin graduación y compás.
Ver video "Polígonos Básicos Regla y compás"Realidad Aumentada OMS: Construcción de polígonos regulares... (1er Grado, Bloque 2)
Haciendo click sobre la imagen, puedes reproducir Realidad Aumentada OMS: Construcción de polígonos regulares... (1er Grado, Bloque 2), un video sobre construir-poligonos-regla-compas publicado por ElMascaraMX el el 05 de julio de 2011. 2.
Ver video "Realidad Aumentada OMS: Construcción de polígonos regulares... (1er Grado, Bloque 2)"Construcción de un polígono regular de 15 lados
Haciendo click sobre la imagen, puedes reproducir Construcción de un polígono regular de 15 lados, un video sobre construir-poligonos-regla-compas publicado por Tareasplus el el 07 de octubre de 2011. Construcción de un polígono regular de 15 lados mediante el uso de regla y compás http://www.
Ver video "Construcción de un polígono regular de 15 lados"Como dibujar un pentagono regular
Haciendo click sobre la imagen, puedes reproducir Como dibujar un pentagono regular, un video sobre construir-poligonos-regla-compas publicado por recetasdecocina el el 21 de septiembre de 2010. En este video tutorial podras aprender a dibujar un pentágono regular dado el lado.
Ver video "Como dibujar un pentagono regular"construcción eneágono regular dado un lado
Haciendo click sobre la imagen, puedes reproducir construcción eneágono regular dado un lado, un video sobre construir-poligonos-regla-compas publicado por Tareasplus el el 29 de septiembre de 2011. Construcción de un eneágono regular mediante regla y compás dado el lado htttp://www.
Ver video "construcción eneágono regular dado un lado"Compás Plano (Alumno) - TRAZO DE POLIGONOS REGULARES A PARTIR DE LADOS Y ANGULOS
Haciendo click sobre la imagen, puedes reproducir Compás Plano (Alumno) - TRAZO DE POLIGONOS REGULARES A PARTIR DE LADOS Y ANGULOS, un video sobre construir-poligonos-regla-compas publicado por Copplano el el 14 de julio de 2011. Dispositivo para el trazo de dibujos.
Ver video "Compás Plano (Alumno) - TRAZO DE POLIGONOS REGULARES A PARTIR DE LADOS Y ANGULOS"Construcción del Heptadecágono regular con Cabri II
Haciendo click sobre la imagen, puedes reproducir Construcción del Heptadecágono regular con Cabri II, un video sobre construir-poligonos-regla-compas publicado por Sabrina Dechima el el 23 de enero de 2012. Construcción de un poligono regular de 17 lados (Resuelto por Gauss a los 19 años de edad).
Ver video "Construcción del Heptadecágono regular con Cabri II"¿como hacer un pentagono regular?
Haciendo click sobre la imagen, puedes reproducir ¿como hacer un pentagono regular?, un video sobre construir-poligonos-regla-compas publicado por RodrigoFlores64 el el 15 de junio de 2009. pentagono geometria regla construccion elaboracion manual explicado pentagono regular ¿como se hace? trabajo esfuerzo humano matematicas planas.
Ver video "¿como hacer un pentagono regular?"Pentágono regular conociendo el lado
Haciendo click sobre la imagen, puedes reproducir Pentágono regular conociendo el lado, un video sobre construir-poligonos-regla-compas publicado por paseoplasticavideo el el 28 de noviembre de 2010. Explicación y desarrollo, paso a paso, de un método para construir un pentágono, polígono regular de cinco lados.
Ver video "Pentágono regular conociendo el lado"Pentágono con regla y compas
Haciendo click sobre la imagen, puedes reproducir Pentágono con regla y compas, un video sobre construir-poligonos-regla-compas publicado por Cristhian Camilo Camacho Sáenz el el 01 de octubre de 2011. Pentágono con regla y compas.
Ver video "Pentágono con regla y compas"GEOMETRIA-Construcciones con Regla y Compás.-
Haciendo click sobre la imagen, puedes reproducir GEOMETRIA-Construcciones con Regla y Compás.-, un video sobre construir-poligonos-regla-compas publicado por Marcela Fierro el el 15 de mayo de 2011. Hola,en este video les enseñare a construir un cuadrado,triangulos y angulos usando bisectrìz.
Ver video "GEOMETRIA-Construcciones con Regla y Compás.-"Dibujo Tecnico: Poligonos regulares por metodo general segun circunferencia circunscrita
Haciendo click sobre la imagen, puedes reproducir Dibujo Tecnico: Poligonos regulares por metodo general segun circunferencia circunscrita, un video sobre construir-poligonos-regla-compas publicado por bjorn512 el el 27 de septiembre de 2012. En este video explico como se trazan poligonos regulares de cualquier numero de lados usando el metodo general.
Ver video "Dibujo Tecnico: Poligonos regulares por metodo general segun circunferencia circunscrita"CONSTRUCCIÓN DE UN OCTÓGONO A PARTIR DEL LADO
Haciendo click sobre la imagen, puedes reproducir CONSTRUCCIÓN DE UN OCTÓGONO A PARTIR DEL LADO, un video sobre construir-poligonos-regla-compas publicado por Aitor Echevarria el el 27 de octubre de 2009. Triángulos.
Ver video "CONSTRUCCIÓN DE UN OCTÓGONO A PARTIR DEL LADO"Dibujo Tecnico: Como dibujar un Heptagono regular con compas escuadra y cartabon
Haciendo click sobre la imagen, puedes reproducir Dibujo Tecnico: Como dibujar un Heptagono regular con compas escuadra y cartabon, un video sobre construir-poligonos-regla-compas publicado por bjorn512 el el 27 de septiembre de 2012. Como dibujar un heptagono regular (7 lados y angulos iguales ) unicamente usando el compas la escuadra y el cartabon.
Ver video "Dibujo Tecnico: Como dibujar un Heptagono regular con compas escuadra y cartabon"Como dibujar un pentagono regular mejorado
Haciendo click sobre la imagen, puedes reproducir Como dibujar un pentagono regular mejorado, un video sobre construir-poligonos-regla-compas publicado por bjorn512 el el 05 de octubre de 2012. En este video explico como dibujar un pentagono regular conocida su circunferencia circunscrita.
Ver video "Como dibujar un pentagono regular mejorado"Construir el triángulo, hexágono y heptágono inscrito
Haciendo click sobre la imagen, puedes reproducir Construir el triángulo, hexágono y heptágono inscrito, un video sobre construir-poligonos-regla-compas publicado por Rubén Ferrer Pérez el el 14 de diciembre de 2010. Obtención de los lados l3, l6 y l7 para poder dibujar el triángulo, el hexágono y el heptágono circunscrito.
Ver video "Construir el triángulo, hexágono y heptágono inscrito"Árbol de los Polígonos
Haciendo click sobre la imagen, puedes reproducir Árbol de los Polígonos, un video sobre construir-poligonos-regla-compas publicado por Guille Pita el el 17 de junio de 2012. Con este vídeo aprenderemos a dibujar un triángulo, un cuadrado, un pentágono, un hexágono, un octógono, un decágono y un dodecágono en un mismo folio, utili.
Ver video "Árbol de los Polígonos"Dibujo tecnico: Como dibujar un Pentagono regular con compas escuadra y cartabon
Haciendo click sobre la imagen, puedes reproducir Dibujo tecnico: Como dibujar un Pentagono regular con compas escuadra y cartabon, un video sobre construir-poligonos-regla-compas publicado por bjorn512 el el 27 de septiembre de 2012. En este video explico como dibujar un pentagono regular a partir de su circunferencia circunscrita, sin transportador de angulos.
Ver video "Dibujo tecnico: Como dibujar un Pentagono regular con compas escuadra y cartabon"Construcción de polígonos regulares y ángulos congruentes
Haciendo click sobre la imagen, puedes reproducir Construcción de polígonos regulares y ángulos congruentes, un video sobre construir-poligonos-regla-compas publicado por Ninette3punto1416 el el 14 de marzo de 2013. Aprenderás cómo construir un polígono regular inscrito en una circunferencia, y cómo trazar un ángulo congruente a otro.
Ver video "Construcción de polígonos regulares y ángulos congruentes"CONSTRUCCIÓN DE UN HEPTÁGONO REGULAR A PARTIR DEL LADO
Haciendo click sobre la imagen, puedes reproducir CONSTRUCCIÓN DE UN HEPTÁGONO REGULAR A PARTIR DEL LADO, un video sobre construir-poligonos-regla-compas publicado por Aitor Echevarria el el 14 de octubre de 2009. POLÍGONOS.
Ver video "CONSTRUCCIÓN DE UN HEPTÁGONO REGULAR A PARTIR DEL LADO"Bisectriz: ángulos de 60 y 30 grados
Haciendo click sobre la imagen, puedes reproducir Bisectriz: ángulos de 60 y 30 grados, un video sobre construir-poligonos-regla-compas publicado por dibujo1011 el el 29 de octubre de 2011. Trazado del ángulo de 60 grados con el compás y bisectriz del mismo, obteniendo el ángulo de 30 grados.
Ver video "Bisectriz: ángulos de 60 y 30 grados"poligonoestrellado.wmv
Haciendo click sobre la imagen, puedes reproducir poligonoestrellado.wmv, un video sobre construir-poligonos-regla-compas publicado por Fernando Díaz Mirón el el 04 de julio de 2011. video tutorial de construcción de polígonos estrellados de 5 puntas.
Ver video "poligonoestrellado.wmv"
Si has llegado a este sitio para saber cuántas diagonales tiene un hexágono, seguro es que necesitas ayuda para tu clase de geometría de la escuela.
Antes que nada, tienes que tener en claro qué clase de figura es un hexágono, para que te sea más fácil calcular la cantidad de diagonales.
Un hexágono es un polígono de seis lados y cuenta con tres diagonales. Pero exite una fórmula que puede descifrar la cantidad de diagonales con las que cuentan lo polígonos y es la siguiente:
En el caso del hexágono, la fórmula es 6 (cantidad de lados)-3, lo que nos da como resultado tres diagonales.
Fuente foto: dtvb.ibilce.unesp.br





Trazados
Dada la circunferencia circunscrita
Sabiendo que la longitud del hexágono inscrito en la circunferencia es igual al radio de la misma, basta trazar seis cuerdas consecutivas de esa longitud.Dado el lado