Numeros Enteros

¿Que son los Numeros Enteros?

Número entero, cualquier elemento del conjunto formado por los números naturales y sus opuestos. El conjunto de los números enteros se designa por Z:

Z = {…, -11, -10,…, -2, -1, -0, 1, 2,…, 10, 11,…}

Los números negativos permiten contar nuevos tipos de cantidades (como los saldos deudores) y ordenar por encima o por debajo de un cierto elemento de referencia (las temperaturas superiores o inferiores a 0 grados, los pisos de un edificio por encima o por debajo de la entrada al mismo…).

Se llama valor absoluto de un número entero a, a un número natural que se designa |a| y que es igual al propio a si es positivo o cero, y a -a si es negativo. Es decir:

• si a > 0, |a| = a ; por ejemplo, |5| = 5;
• si a < 0, |a| = -a ; por ejemplo, |-5| = -(-5) = 5.

El valor absoluto de un número es, pues, siempre positivo.

Las operaciones suma, resta y multiplicación de números enteros son operaciones internas porque su resultado es también un número entero. Sin embargo, dos números enteros sólo se pueden dividir si el dividendo es múltiplo del divisor.

Suma de Numeros Enteros

Para sumar dos números enteros se procede del siguiente modo:

• Si tienen el mismo signo, se suman sus valores absolutos, y al resultado se le pone el signo que tenían los sumandos:
• 7 + 11 = 18
• -7 - 11 = -18
• Si tienen distintos signos, es decir, si un sumando es positivo y el otro negativo, se restan sus valores absolutos y se le pone el signo del mayor:
• 7 + (-5) = 7 - 5 = 2
• -7 + 5 = - (7 - 5) = -2
• 14 + (-14) = 0

La suma de números enteros tiene las propiedades siguientes:

Asociativa:
(a + b) + c = a + (b + c)
Conmutativa:
a + b = b + a
Elemento neutro: el cero es el elemento neutro de la suma,
a + 0 = a
Elemento opuesto: todo número entero a, tiene un opuesto –a,
a + (-a) = 0

Multiplicacion de Numeros Enteros

Para multiplicar dos números enteros se multiplican sus valores absolutos y el resultado se deja con signo positivo si ambos factores son del mismo signo o se le pone el signo menos si los factores son de signos distintos. Este procedimiento para obtener el signo de un producto a partir del signo de los factores se denomina regla de los signos y se sintetiza del siguiente modo:
+ · + = +
+ · - = -
- · + = -
- · - = +

La multiplicación de números enteros tiene las propiedades siguientes:
Asociativa:
(a · b) · c = a · (b · c)
Conmutativa:
a · b = b · a
Elemento neutro: el 1 es el elemento neutro de la multiplicación,
a · 1 = a
Distributiva de la multiplicación respecto de la suma:
a · (b + c) = a · b + a · c

Resta de Numeros Enteros

Para restar dos números enteros se le suma al minuendo el opuesto del sustraendo:
a - b = a + (-b)

Por ejemplo:
5 - (-3) = 5 + 3 = 8
-2 - 5 = (-2) + (-5) = -7

Cómo sumar y restar números enteros negativos

Un entero negativo es esencialmente un número entero negativo. Enteros no incluyen decimales y fracciones, pero sí incluyen cero. La sustracción y suma básica de números enteros negativos es una habilidad que a menudo se aprende en la escuela y es esencial para algunas personas en su carrera. Algunos trabajadores, tales como contadores, trabajan en estrecha colaboración con los números y conocer como restar y sumar enteros negativos es esencial. Aunque el proceso puede ser algo confuso al principio, el tiempo y la práctica son esenciales para comprender plenamente cómo sumar y restar números enteros negativos.

Instrucciones

Dibuje una línea horizontal en una hoja de papel. Marque el centro de la línea con el valor cero. Marque números enteros positivos en el lado derecho de la línea y números enteros negativos en el lado izquierdo comenzando con 1 y -1. Esto crea una línea de números.

Reste dos números enteros negativos como -5 y -3. Restar dos números enteros negativos tiene el mismo resultado que sumar el valor positivo del número que se resta, ya que los dos signos negativos se eliminan entre sí. Por lo tanto, el resultado de -5 - (-3) es de -2. Inicie en el valor -5 en la recta numérica y muévase tres enteros a la derecha para obtener el resultado.

Sume dos números enteros negativos, tales como -4 y -8. La adición de dos enteros negativos es similar a la adición de dos números enteros positivos. El resultado obtiene un valor negativo. Comience en el valor -4 y muévase ocho enteros a la izquierda. El resultado de -4+ (-8) es de -12.

Si deseas leer más artículos parecidos a cómo sumar y restar números enteros negativos, te recomendamos que entres en nuestra categoría de Educación Matemática.

Sigue leyendo: http://educacion.uncomo.com/articulo/como-sumar-y-restar-numeros-enteros-negativos-716.html#ixzz2MfXV73u7

Los Números Enteros

LOS NÚMEROS ENTEROS
¿Como puedes diferenciar una deuda de 24 bolívares con un ingreso de 24 bolívares? Con los números naturales no es suficiente, es por ello que resulta necesario introducir otro tipo de números: los números enteros, colocando un signo + o - delante cada número. Para cada sustitución se establece un nivel 0, un sentido positivo (+) y un sentido negativo (-), pero casi siempre los enteros positivos se representan sin el signo +.
En los vuelos espaciales se toma el tiempo 0 el momento de lanzamiento. Por consiguiente, -20 segundos significa 20 segundos antes del lanzamiento, y +8 querrá decir que han pasado 8 segundos después del lanzamiento
El conjunto de  los números enteros, se denota con la letra Z, y está formado el conjunto de los números enteros positivos, los números enteros negativos  y el cero que se representa de la siguiente manera:
Z: {…….., -3, -2, -1, 0, +1, +2, +3,………}
En el conjunto de los números enteros se pueden distinguir algunos subconjuntos notables, estos son:
El conjunto de los números enteros positivos, denotado por Z⁺ :
Z⁺ = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12…}
El conjunto de los números enteros negativos, denotado por Z^- :
             Z^- ={…-10, -9, -8, -7, -6, -5, -4, -3, -2, -1}
El conjunto de los números enteros diferentes de cero, denotado por Z^* :
              Z^* = {…, -6, -5, -4, -3, -2, -1, +1, + 2, + 3, +4, +5, + 6,… }

18/03/2011 01:46 NUMEROS ENTEROS Z Enlace permanente. sin tema No hay comentarios. Comentar.

Representacion Gráfica de un Número Entero

Representación gráfica de un número entero
Los números enteros se representan en una recta numérica por medio de puntos ubicados a igual distancia, a la derecha y a la izquierda, de un punto determinado por el número 0 de la siguiente forma:
18/03/2011 01:45 NUMEROS ENTEROS Z Enlace permanente. sin tema No hay comentarios. Comentar.

¿Y esta publicidad? Puedes eliminarla si quieres

Valor Absoluto de un Número Entero.

Valor absoluto de un números entero
Observa la recta númerica
Los números están ubicados a la misma distancia del cero, el valor absoluto de un número entero es la distancia que hay desde un número hasta el cero, para indicar el valor absoluto de algo se coloca el símbolo “|” a cada lado del numero por ejemplo:
a) |-5|= 5                                        b) |7|=7

Calcula el valor absoluto delas siguientes expresiones:
a)   |+75|=
b)   |-82 |=
c)   |-10 |=
d)   -|+59|=
18/03/2011 01:40 NUMEROS ENTEROS Z Enlace permanente. sin tema No hay comentarios. Comentar.

Operaciones con Números Enteros.

Operaciones con Números EnterosEn el conjunto de los números enteros se definen las siguientes operaciones: suma, resta, multiplicación y división. Suma y Resta de Números EnterosPara sumar números enteros se debe tomar en cuenta los signos; si los números enteros son de igual signo, se suman los valores y coloca el mismo signo de los sumandos.Ejemplo:a)   5+3 = 8                  b) (-7)+ (-2)= -9Si los números enteros son de diferentes signos, se restan los valores y coloca el signo del  sumando mayor.Ejemplo:a)   9+(-3)=6               b) (-12) +5 = -7A partir de esta operación se define la resta de números enteros, como la suma del opuesto: a - b= a+ (-b)Ejemplo:(-3)-(-5)= -3+5= 218/03/2011 01:29 NUMEROS ENTEROS Z Enlace permanente. sin tema No hay comentarios. Comentar.

Operaciones con Números Enteros.

Multiplicación y división de Números EnterosMultiplicación de Números EnterosLa multiplicación de dos números enteros da como resultado otro número entero, para ello se procede de la siguiente manera: primero se multiplican los factores y luego se multiplican los signos . El signo de los resultados es positivo cuando los factores tienen el mismo signo, y negativo si tienen signos distintos( tabla de signos)Tabla de signos

+	.	+	+
+	.	-	-
-	.	+	-
-	.	-	+

Ejemplos:
a) 2.3= 6                               b) 4 . (-3) = -12
b) (-5). (-2) = 10                    d) (-7) . 6 = -42

División de Números Enteros
Para hallar el cociente de dos números enteros, se dividen los valores y los signos; si el dividendo y el divisor tienen el mismo signo el cociente es positivo, y si el dividendo y el divisor tienen diferentes signos, el cociente es negativo.
tabla de signos

 

 

3. Números enteros

Editar 0 0 8…

NÚMEROS ENTEROS: WEBQUEST

EL ASCENSOR

LA RECTA ENTERA.

COMPARACIÓN DE NÚMEROS ENTEROS

 

Qué son los Números Enteros?

Hoy vamos a hablar de los números enteros, los cuales pueden ser muy bien reconocidos por cualquiera de nosotros por poder mantener dentro a todos los números que sean positivos, negativos y el cero. Lo único que hay que tomar muy en cuenta es que los naturales no tienen porqué ser representados como si se trataran de una fracción o poseyendo decimales, sui representación gráfica debe ser tan solo el número que deseamos representar y en caso de ser un negativo vamos a necesitar colocarle un símbolo de resta hacia su lado izquierdo para denotar el carácter contrario hacia los números positivos, a los cuales si se desea bien se le podría colocar un símbolo de suma. Además tengamos en cuenta que los enteros son representados simbólicamente por la letra ℤ, la cual viene del alemán Zahlen (‘números’).

Vale la pena mencionar que los números enteros se dividen en pares e impares. Los pares son aquellos que son múltiplos de 2. Algunos ejemplos, son 2,4,6,8,10, etc. También podemos encontrar numeros pares negativos como -2,-4,-6,-8,-10, etc.
Por su parte los números impares son números enteros que no son múltiplos de 2. Entre ellos encontramos al 1, 3, 5, 7, 9, etc. En el caso de los negativos podemos mencionar al -1, -3, -5, -7, -9, etc.
Ahora que ya sabes qué son los números enteros, te dejamos un video para comprender a cabalidad lo que te explicamos: Números Enteros

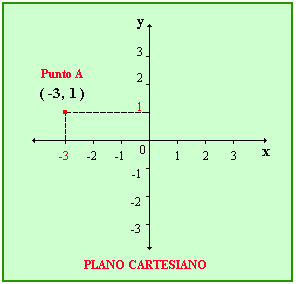
• NÚMEROS ENTEROS Operaciones con números enteros Para indicar si un objeto se encuentra a la derecha o a la izquierda de un punto de referencia, podemos indicar con un signo + si está hacia la derecha y con un signo - si se ubica hacia la izquierda. De esta forma obtenemos dos conjuntos: - Conjunto de números positivos - Conjunto de números negativos El conjunto formado por los números positivos, los números negativos y el cero se llama conjunto de números enteros. 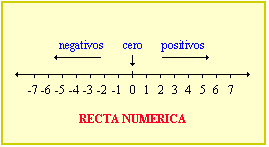  Sumas y restas entre números enteros
  Los comerciantes europeos usaban los signos "+" y "-" para diferenciar las ganancias de las pérdidas o deudas. De allí fue que los matemáticos adoptaron estos signos y, comenzaron a escribir 5 + 10 en vez de Esto era lo que se usaba antes de usarse el signo "+" : "p'' era el símbolo de la suma, pues la palabra "plus'' significa en latín "más''. Así, cuando en Europa se comenzaron a usar los números que representaban deudas, se les asignó el signo "-'' adelante.
  Se comenzará por observar que una resta entre números naturales puede interpretarse de la siguiente manera, usando los números negativos:   Si se piensa que el número negativo -6 representa una deuda en bolívares, está claro que al tener 10 Bs. más una deuda de 6 Bs., el saldo es de 4 Bs., y esto es lo que se obtiene al restar 10 -6. Así, siempre que se tenga que realizar una resta , puede escribirse como la suma del minuendo más el opuesto del sustraendo.
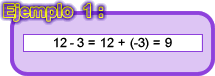
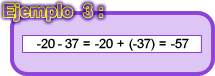
  En esta operación última la resta podría parecer un poco extraña: un número negativo menos un número positivo. Si la escribimos como suma del minuendo más el opuesto del sustraendo, se obtiene una suma de dos números negativos. Podría decirse, la suma de dos deudas. Ciertamente, eso lo que da es una deuda mayor que las anteriores. ¿Exactamente a cuánto alcanza la deuda?
  Naturalmente, se suman 20+37=57 y eso da la cantidad que se debe, es decir,
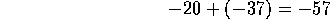
  Veamos ahora este caso: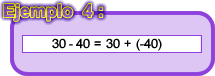
  En este caso, debe restarse a 30 un número mayor, que es 40. Si se interpreta como la suma de 30 + (-40) , se puede realizar esa operación, cosa que no podía hacerse cuando no se conocían los números negativos. Volviendo a pensar en deudas, se tiene 30 Bs. y una deuda de 40 Bs. Eso significa que se paga lo que se tiene y se siguen debiendo 10 Bs. Es decir: Ahora se sabe que cualquier resta se puede interpretar como una suma (el minuendo más el opuesto del sustraendo). Bastará entonces con aprender bien a realizar la SUMA de números enteros, para poder realizar cualquier suma o resta de números enteros. Como los números enteros pueden ser positivos o negativos, se estudiarán los casos que es posible encontrar:
  Suma de dos enteros positivos: Se realiza como hasta ahora se han sumado dos números naturales:
  Suma de dos enteros de signos contrarios: Cuando se suman dos números de signos contrarios, se está en presencia de una ganancia y una pérdida; se sabe bien que si la pérdida es mayor que la ganancia, lo que queda al final es una deuda, y si, por el contrario, la ganancia es mayor que la pérdida, lo que queda es ganancia. De esta manera, se ve que el signo del resultado de sumar dos números de signos contrarios es el signo del mayor de los números, si ambos fueran positivos.
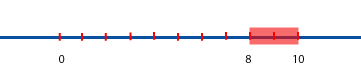
  Podría interpretarse la suma del ejemplo como la operación de "moverse" 8 unidades a la derecha de -10. Se puede ver que, como 8 es menor que 10, al moverse uno 8 unidades a la derecha, no alcanza al cero. Faltarían 2 unidades para alcanzar al cero. Es decir, se llega hasta -2.
  	El monto total de pérdida o ganancia en cada caso será la diferencia entre los números, ignorando el signo.
  En el ejemplo 5: -10+8=-2 porque la diferencia entre 10 y 8 es 2.
  En el ejemplo 6: 11+(-8)=3 porque la diferencia entre 11 y 8 es 3.
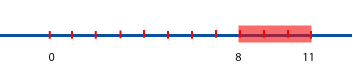
  De nuevo, puede interpretarse esta suma como el resultado de moverse desde 11, hacia la izquierda, 8 unidades. Otros ejemplos:
  -5+7=2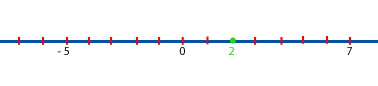
  3+(-1)=2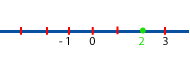
  9+(-12)=-3
  En los ejemplos citados al comienzo, se tienen sumas de números con signos contrarios. Se tiene El resultado 9, lleva el signo positivo porque 12 tiene signo positivo. En 2), igualmente tenemos En cambio, en 4), el mayor de los dos números (sin tomar en cuenta el signo) entre 30 y (-40) es 40. En la suma original, tiene signo negativo, por lo tanto, al restar 40-30, para efectuar esa suma, debemos colocarle el signo negativo al resultado.
  Si has acertado en todas tus respuestas, ¡felicitaciones! has hecho un buen avance, y eso te permitirá seguir aprendiendo lo que sigue sin dificultades.   Si no has realizado correctamente alguno de los ejercicios, revisa de nuevo los ejemplos que se han dado antes, para que asimiles mejor las ideas expuestas.
  Suma de dos enteros negativos: Si tenemos que sumar, por ejemplo, -9 + (-3) , ya sabemos que la suma de dos deudas es una deuda, en este caso igual a: Veamos otros ejemplos: Hemos dicho antes que el opuesto de un número entero es aquel que, sumado a nuestro número, nos da el cero:
  El opuesto de 5 es -5, pues 5 + (-5) = 0 El opuesto de 3 es -3, pues 3+ ( -3) = 0 El opuesto de -7 es 7, pues -7 + 7 = 0 El opuesto de -1 es 1, pues -1+1 = 0
  Es claro que dado cualquier entero positivo, para encontrar su opuesto, basta con anexarle un signo - por delante. Por ejemplo: el opuesto de 8 es -8. El signo -, delante de cualquier expresión matemática, significa el opuesto de esa expresión. Por ejemplo: el opuesto de -6 es -(-6)=+6. Por otra parte, como se acaba de ver en los ejemplos anteriores, para encontrar el opuesto de un número negativo, basta con eliminar el signo - del número. Por ejemplo: el opuesto de -9 es 9. Viendo estas cosas desde el punto de vista de las deudas y las ganancias, es natural pensar que lo opuesto de una deuda es una ganancia de esa misma magnitud: Es muy importante tener presente lo que cada símbolo matemático significa. Aprender Matemáticas se parece a aprender un idioma nuevo. Si no se comprende lo que significa cada palabra de una frase, no se puede entender la frase. Entre los símbolos importantes en el lenguaje de las matemáticas está el signo -. Como se dijo antes, no debe olvidarse su significado: se usa para expresar el opuesto de cualquier expresión que le siga. Si se quiere calcular lo siguiente: Aquí es importante decir que el paréntesis sirve para especificar lo siguiente: todo lo que está dentro del paréntesis está afectado por el signo negativo. Si se tiene en cuenta el significado de esa expresión matemática, no habrá dificultad alguna, pues basta con calcular lo que está dentro del paréntesis, y luego encontrar su opuesto, porque eso es lo que indica el signo - delante de todo. Entonces, 76+32=108, y el opuesto de 108 es -108, por lo tanto,
  Otros ejemplos: Ahora, ocurre algo muy simpático con estos ejemplos, y es que se pueden hacer los cálculos de otra manera y obtener el mismo resultado. Con mucha frecuencia en Matemáticas ocurre esto: hay más de una forma correcta de resolver los problemas y ejercicios. Se verá cuál es esa otra forma en este caso. En el primer ejemplo, en lugar de calcular, como se hizo antes, en primer lugar lo que está dentro del paréntesis, es posible deshacerse del paréntesis primero, haciendo "entrar" al signo -, permitiéndole actuar sobre cada número, así: El signo -, al entrar en la expresión dentro del paréntesis, se coloca delante de cada número que encuentra a su paso, y luego se realizan las operaciones indicadas. Se calcularán los otros ejemplos, haciéndolo de esta misma manera:
  Signos de agrupación Algunas veces se hace necesario realizar operaciones de suma y resta con más de dos números enteros, por ejemplo: Los signos (paréntesis), (corchetes) y (llaves) son llamados signos de agrupación y su papel en las expresiones como la anterior, es el mismo que el de los paréntesis, explicado ya. La diferencia entre un signo de agrupación y otro es sólo que se usan en este orden: el más interno: paréntesis, luego viene el corchete, y el más externo es la llave. Un signo - delante de un paréntesis o de un corchete, o de una llave, indica que se tomará el opuesto de todo lo que hay dentro del signo de agrupación. Deberán, entonces, realizarse las operaciones que están dentro de cada signo de agrupación y luego cambiarse el signo en este caso. Si el paréntesis, el corchete o la llave están precedidos por un signo +, no se cambia el signo de lo que está dentro de los signos de agrupación. Para realizar la operación anterior, se comienza por operar con lo que hay dentro de los signos de agrupación más internos: los paréntesis. Así la expresión se transforma en Ahora se calcula lo que hay dentro de los corchetes: y se escribe Resolviendo las operaciones dentro de las llaves, se obtiene y así la expresión original es igual a Operaciones con Números Enteros Articulo con 23.868 Visitas.Creado el 13 diciembre, 2009 por José M. de la Rosa Sánchez En esta ficha se trabaja la suma y resta de números enteros. En algunas de las operaciones planteadas hay multiplicaciones por lo que es aconsejable que el alumnodo ya conozca la reglas de los signos. La solución y un enlace para jugar con Bob esponja al final del artículo. HAZ CLIC PARA AMPLIAR Si quieres pasar un buen rato con Bob Esponja haz clic en el siguiente dibujo y podrás disfrutar un rato con los juegos de la página oficial. También te puede interesar... Juego "barquitos cartesianos"Sumas y restas posicionalesComplementos del 10Sumas y Restas con decenas, unidades y números completos Números enteros Al ser humano se le presentaron diferentes situaciones:¿Cómo indicar temperaturas bajo 0? ¿Cómo diferenciar alturas y profundidades de la tierra? ¿Cómo expresar que quedó debiendo algo? Al no poder dar respuesta a estas situaciones utilizando los números naturales, se vio en la necesidad de crear un nuevo conjunto de números: los enteros. Los números enteros están formados por los enteros positivos, los enteros negativos y el cero. El 0 no se considera ni positivo ni negativo, es neutro. Los números enteros negativos expresan cantidades que son menores que cero y los enteros positivos cantidades mayores que cero. Los números enteros no tienen parte decimal. El conjunto de los números enteros se simboliza con la letra Z.